





2022-06-30 09:53:56 点击:[]
你的童年是否也玩过这样的玩具呢?齿轮在空心外图板的圆洞中转动,便在纸上绘制出了不同形状的花型曲线呢?这就是我们今天要来说说的万花尺和繁华曲线。
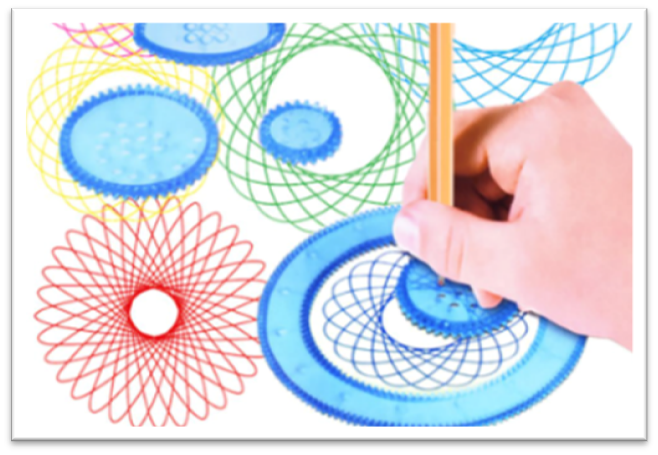

繁花曲线是由获得过我国国家发明家的杨秉烈先生发明的。先生的后半生发明和设计的繁花曲线规,也成为了一代人童年的记忆。老先生已于2007年去世,我们也向老先生致以深深的敬意。
我们都有一个深刻的体会,当铅笔踩着不同的位置,在齿轮之间滑动时,都会呈现不同结构的繁花曲线,这也是小时候我们为何会如此热衷和好奇的原因。那么这种现象是何种原因造成的呢?
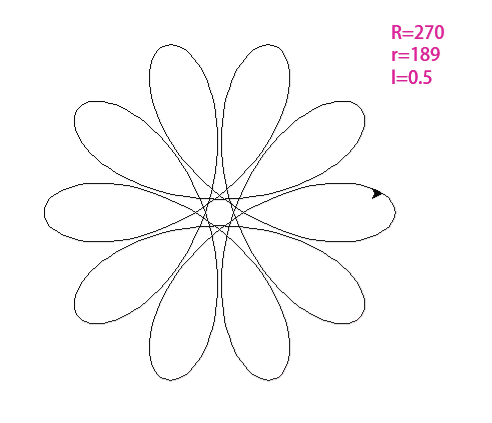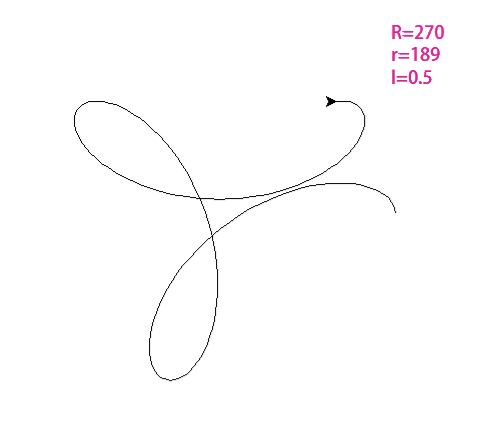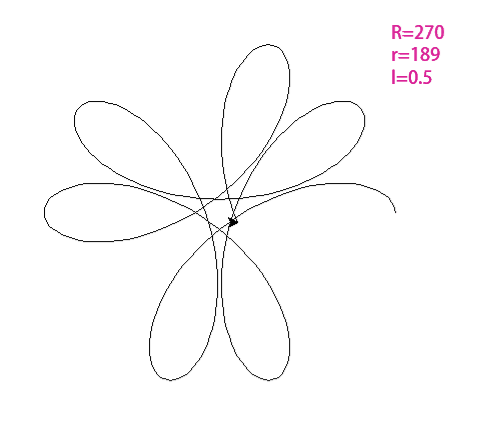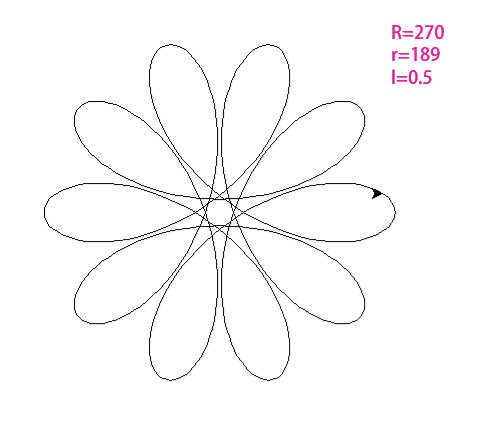
其实,繁花曲线也可以看成是一种特殊的函数,它的结构我们可以用我们学过的参数方程表示,即:
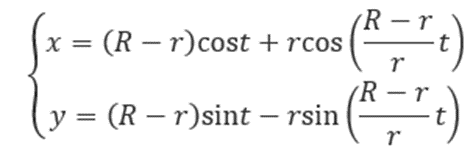
这里的R就是外侧大圆的半径,r是内部齿轮上铅笔所在位置形成的小圆的半径,t是我们绘制过程中转过的角度。
因此,不同的绘制位置,决定了参数,从而导致了形状的变化。下面通过一些编程软件来复现一下绘制的过程和不同参数组合下的繁花曲线。
繁花曲线在工程问题和实际生活中也有所应用。我们将半径分别设置为R=4,r=1,这时候得到的就是星形线,如图所示:
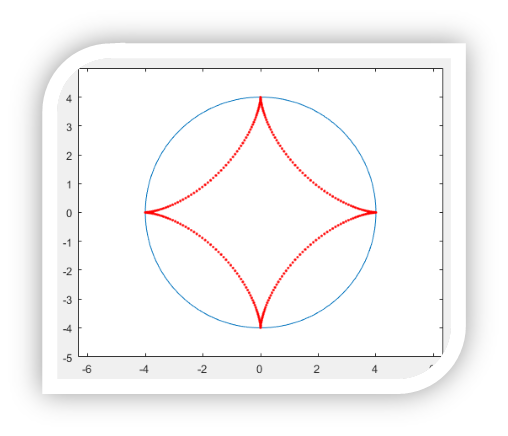
星形线是包络线的其中一种,让定长线段的两个端点在坐标轴上滑动,并保留这些线段,星形线就是这组线段的边界曲线。在数学上我们称为包络线。
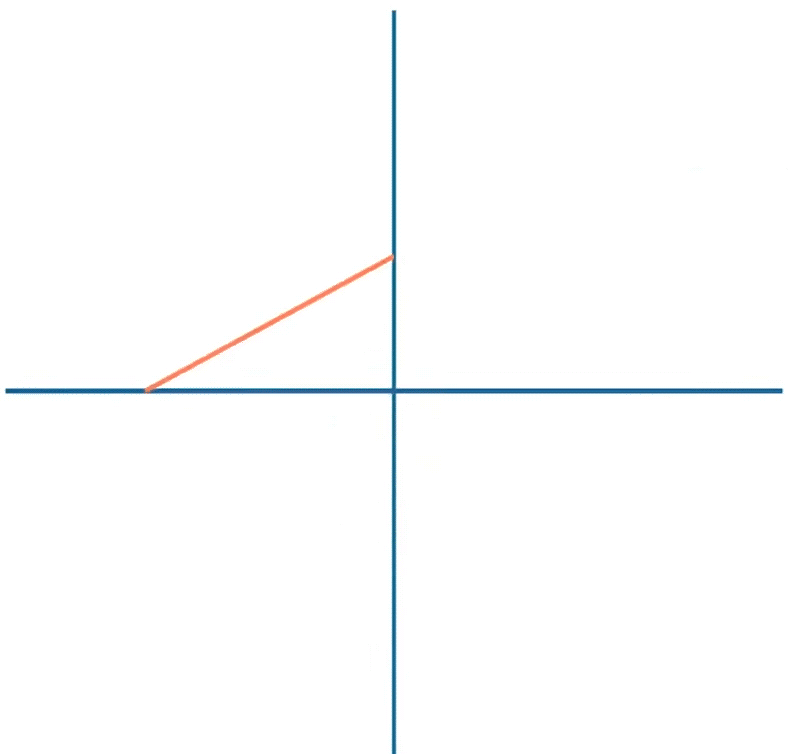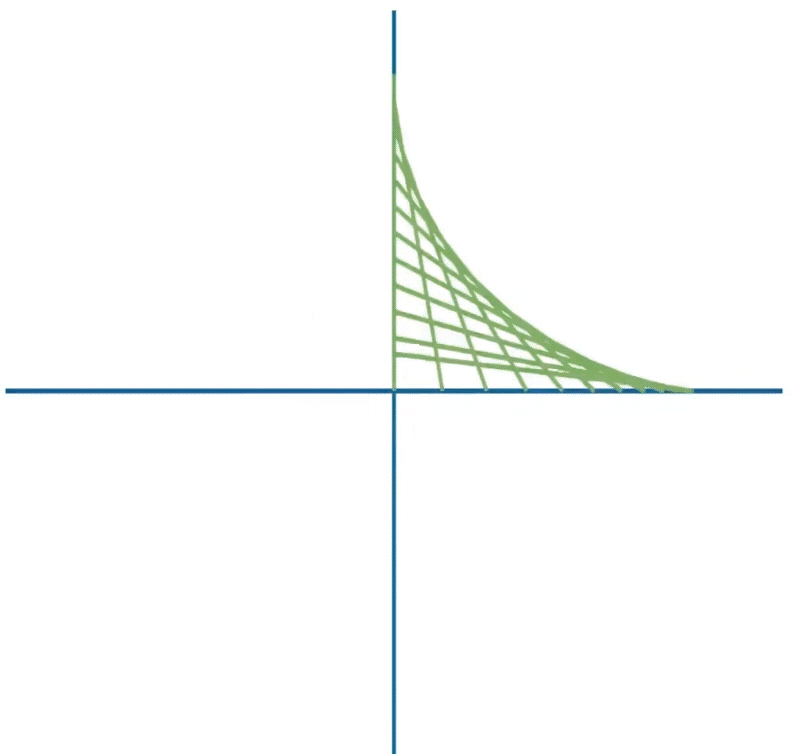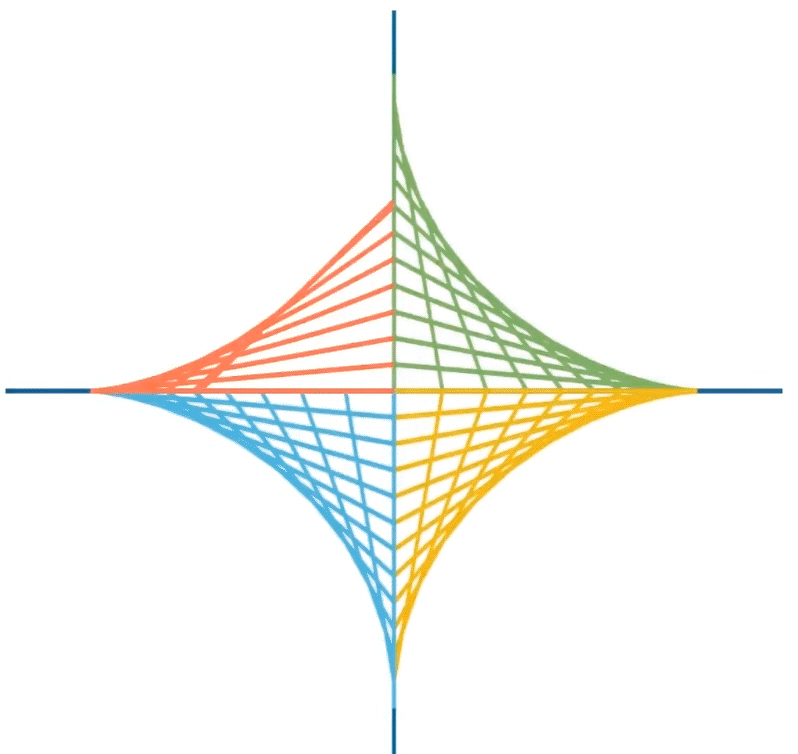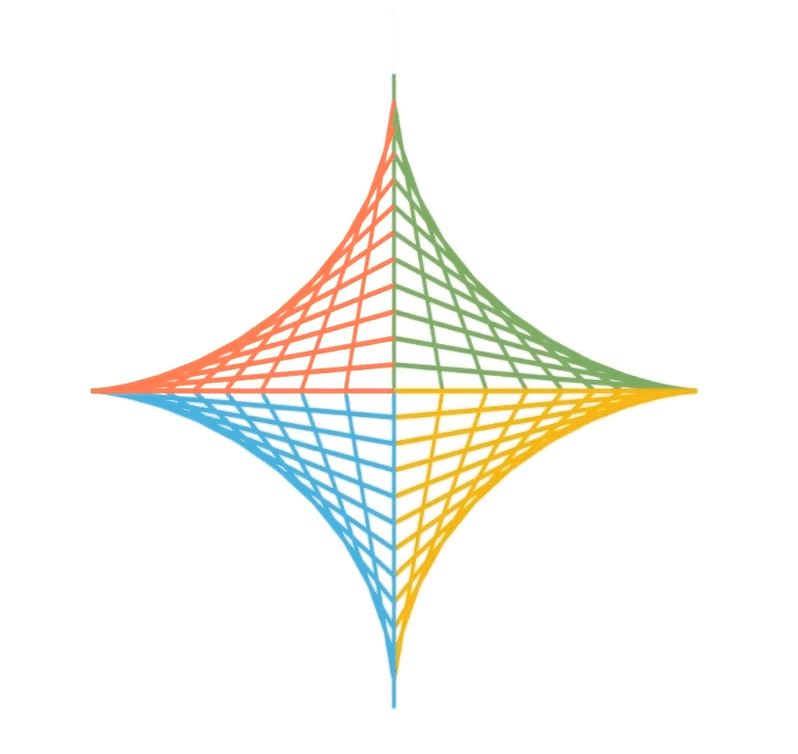
我们在坐公交车时,经常会看到公交车车门使用久了以后,会在地面上留下黑色的痕迹。

在公交车的开关门设计中,我们经常会遇到两种方式,内开门和外开门两种模式。这里的开关门时候在地面上扫过的痕迹就是刚刚的星形线。
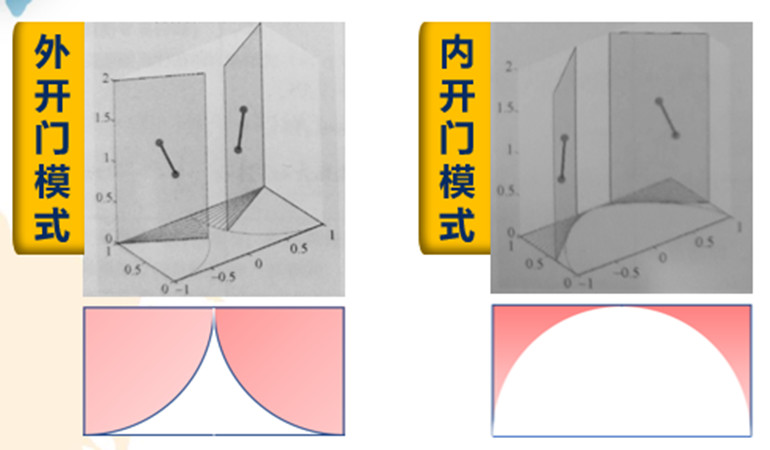
如果你是公交车设计师,你会选择何种开门方式?
内开门节省了开门所占用的空间,又能有效降低在开关门过程中打到乘客的风险,另外从工程角度出发内摆门还具有结构简单,方便维修的优势。
当然随着科学技术的不断进步,现如今当然也涌现了更好的开关门方式,也提升了我们的生活幸福感。
上一条:厦门华厦学院刘海翔教授在《厦门日报》发表文章,讲述华厦校园故事 下一条:科普专题:大自然中的雪花,周长和面积知多少? ——科赫雪花与数列的极限