大自然中无不体现着数学之美，图中的雪花形状值得我们好好来研究一番。它的生长过程如何定义？我们又是否能够通过一些方法求解它的周长和面积呢？我们进入今天的故事。
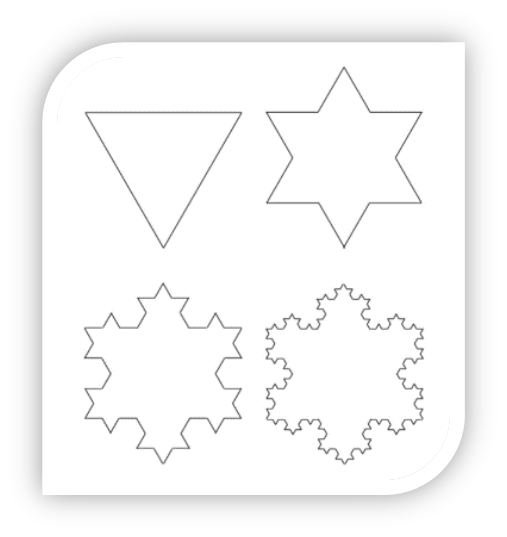
上述图像中的“雪花”在数学中我们定义为科赫雪花。它的生长规则是：
从一个正三角形出发，把每条边三等分，然后以各边的中间部分1/3的长度为底边，分别向外作正三角形，再把“底边”线段抹掉。得到一个“六角星”；
再把每条边三等分，以各中间部分的长度为底边，向外作正三角形后，抹掉底边线段。
反复进行这一过程，就会得到一个类似于“雪花”的图形。我们将这种雪花称为“科赫雪花”。如图。
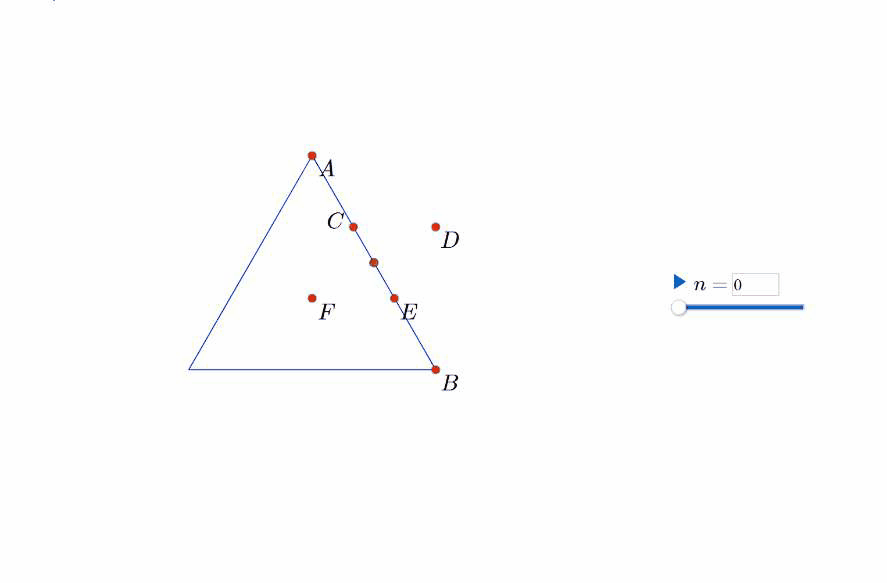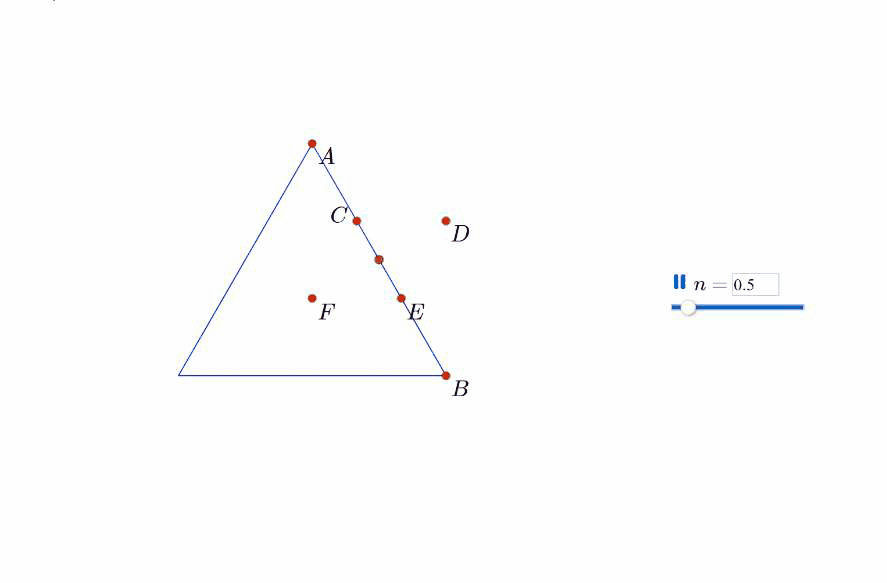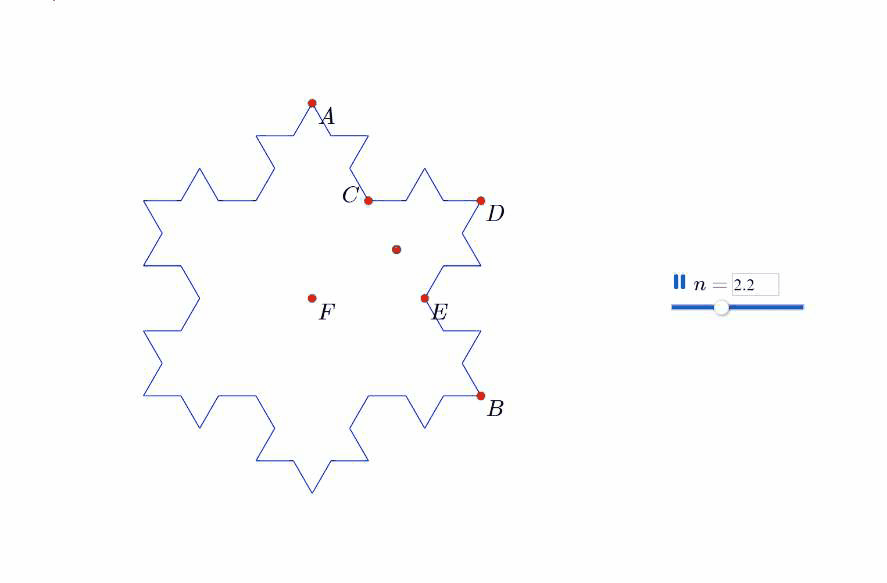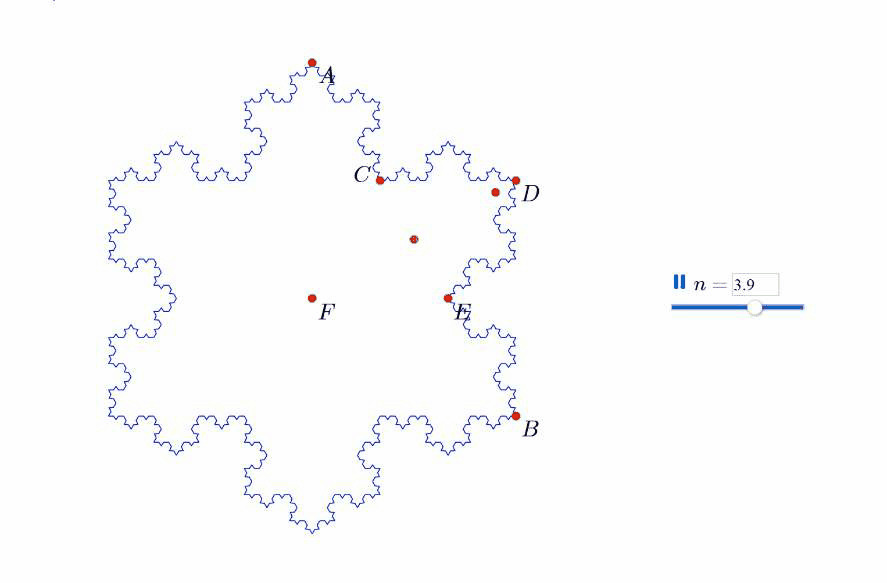
我们来讨论上述生长过程随着n的增加而产生的变化过程。我们可以肯定每次增加的三角形的数量和边数有关，每条边每次增加一个小三角形，每次变化中一条边变出四条边。
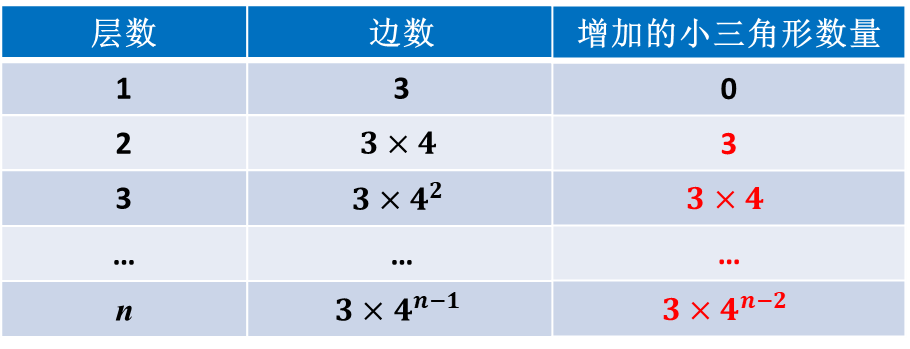
一、周长
假设初始正三角形的周长为
，根据递推关系：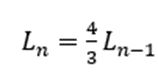
。（对周长的推导过程感兴趣的同学看下图）
科赫雪花的周长数列为：
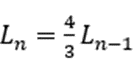
那么n增加，趋于无穷，雪花的周长是否有极限呢？这显然就成为了我们关心的问题。即：
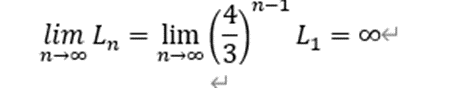
二、面积
设科赫雪花第n层对应的面积值为
,且假设
;
1.每次增加的小三角形的面积是上一层三角形的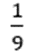
。
2.
面积值是在
的基础上加上3个小三角形的面积，即：
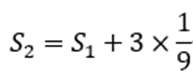
3.递推关系：
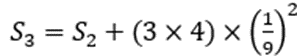
我们通过这个情况可以反复的推导上述的递推关系。
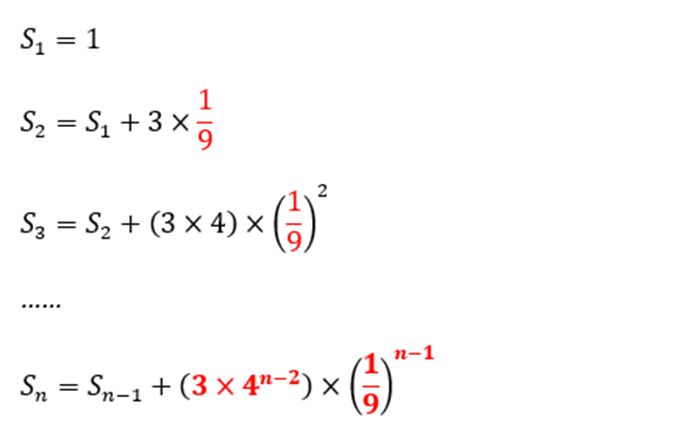
我们通过递推关系就可以求出第n层对应的面积值为
（详细推导看下图）。最终我们可以得到面积的极限。
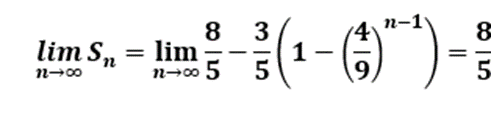
综上所述：如果让科赫雪花无限生长下去，科赫雪花是一个无限大周长，但却有有限的面积的几何图形。
三、数列与我们的生活
像数列和数列的极限在生活中还有许多的应用。
1、在艺术创作和设计中的数列
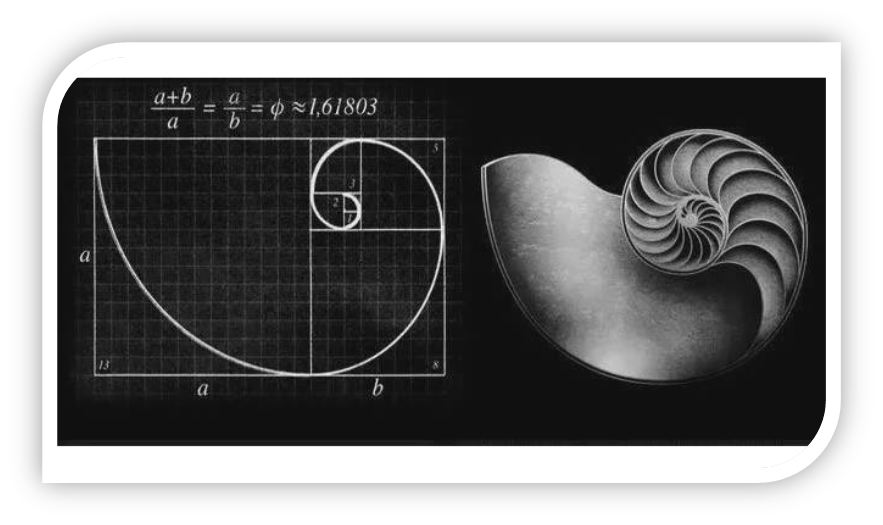
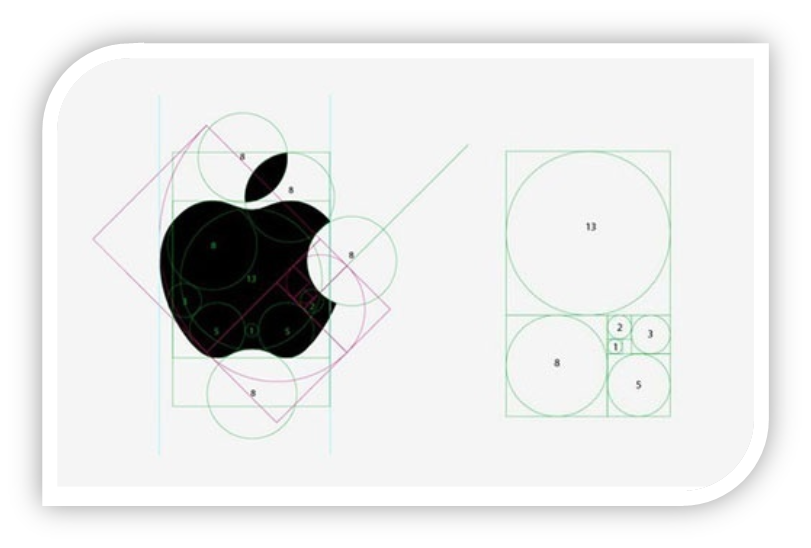
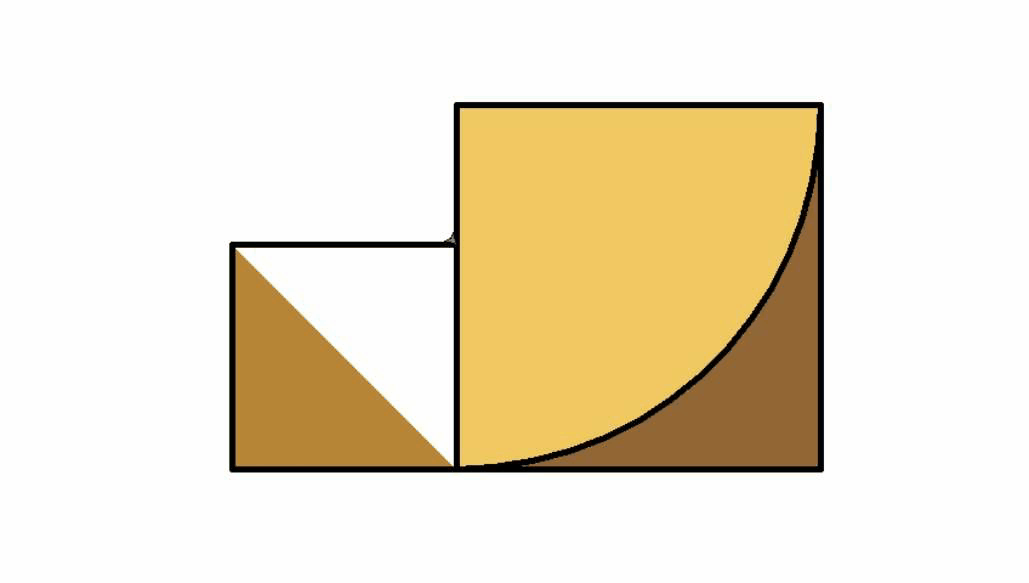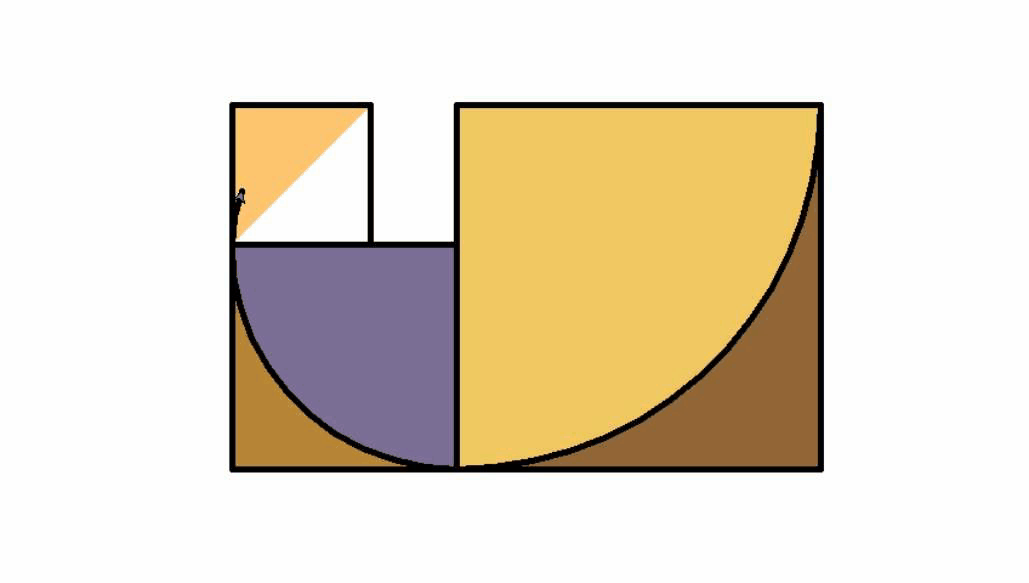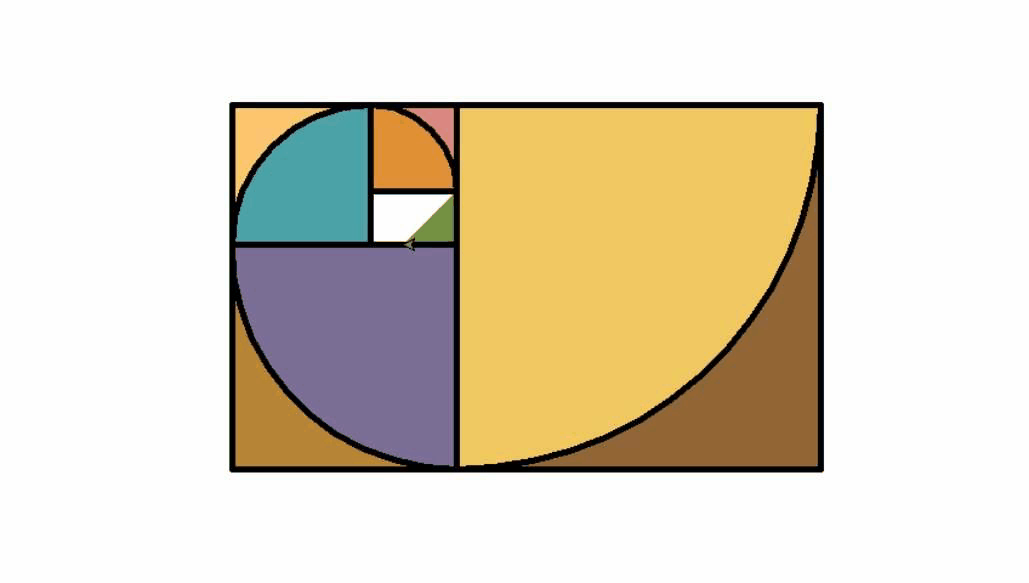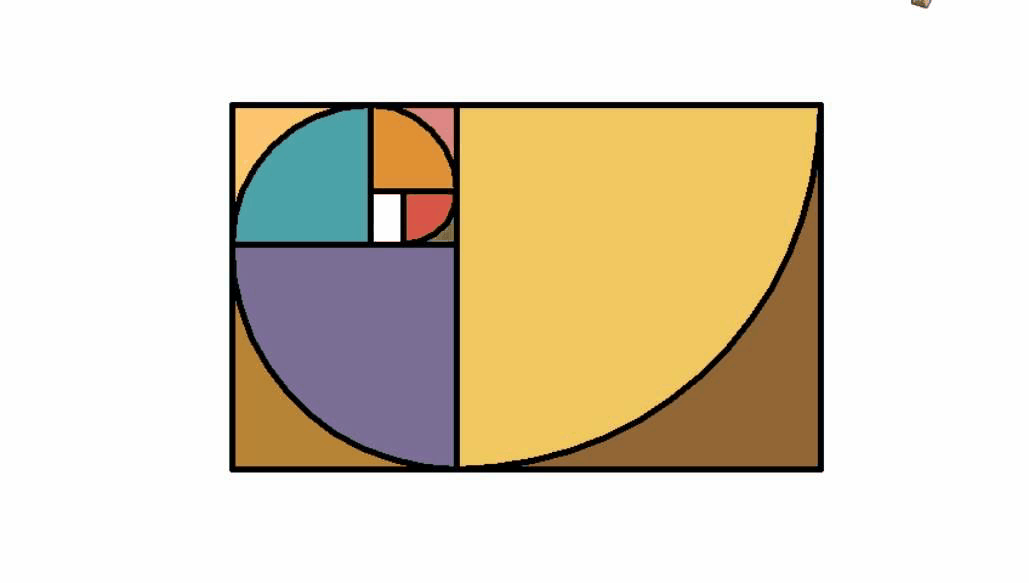
著名的斐波那契数列可以生成螺旋形状线。大自然中的花朵，螺的形状都和其有关，我们手机APP的圆角矩形也与之相关。著名的斐波那契数列其极限正是黄金分割数。
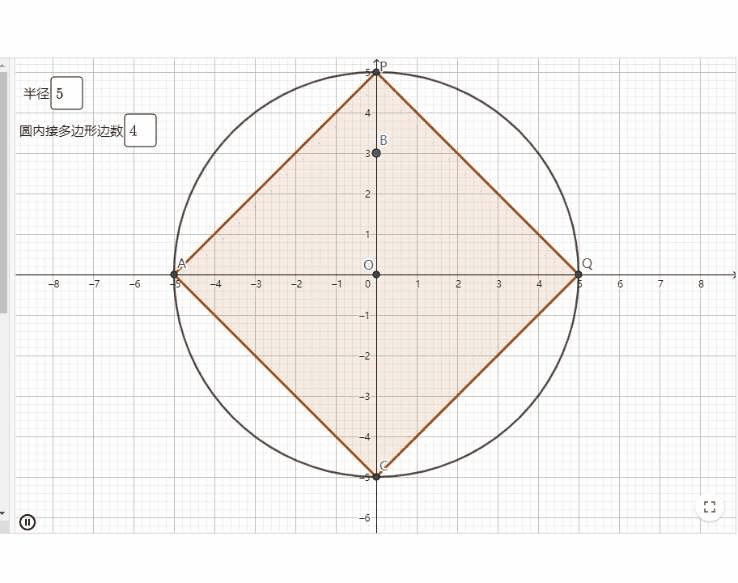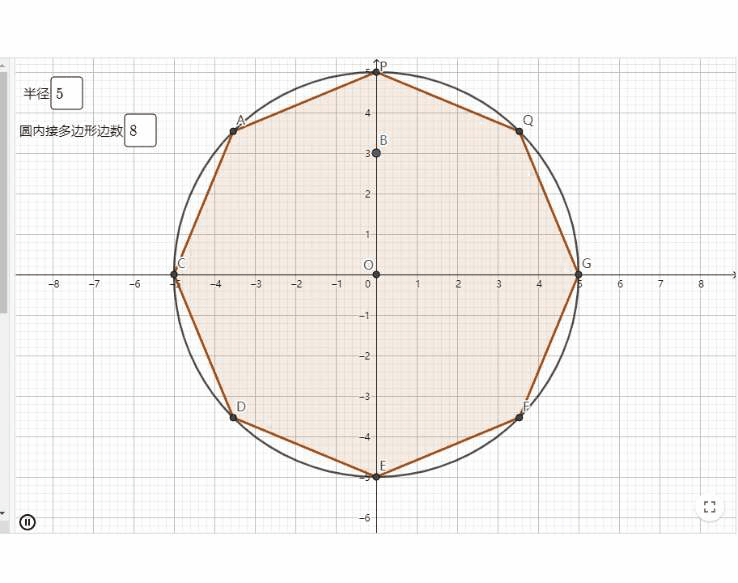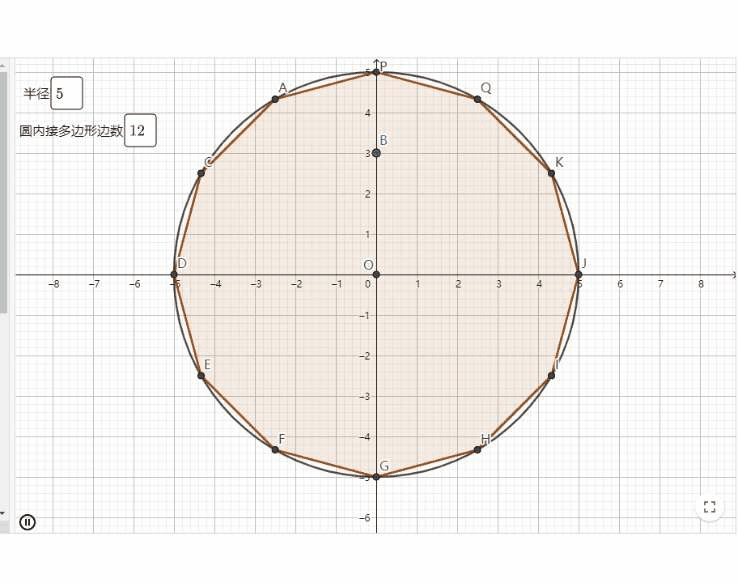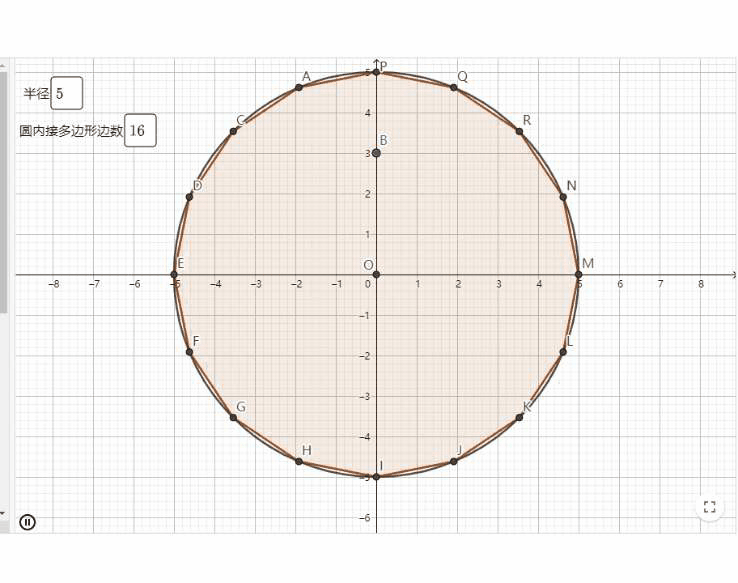
1、刘徽的割圆术计算圆周率
魏晋时期的数学家刘徽提出的割圆术，“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体而无所失矣”。其核心思想就是圆的内接正n边形面积所构成的数列，其极限就是圆的面积。
刘徽把圆内接正多边形的周长一直算到了正3072边形，并由此而求得了圆周率为3.1415和3.1416这两个近似数值。这个结果是当时世界上圆周率计算的最精确的数据。
