科普专题：比一比：谁会更快的从等高处下降至地面呢？

一、最速降线情景展示

开始今天的故事前，请大家观察下面这个图，各种颜色的轨道上都会有一个球从A点出发，那么我们不禁发问，哪条轨道上的球会最先到达B点。

同学们可以先猜猜会是哪条颜色轨道上的球能最快下降到B点？

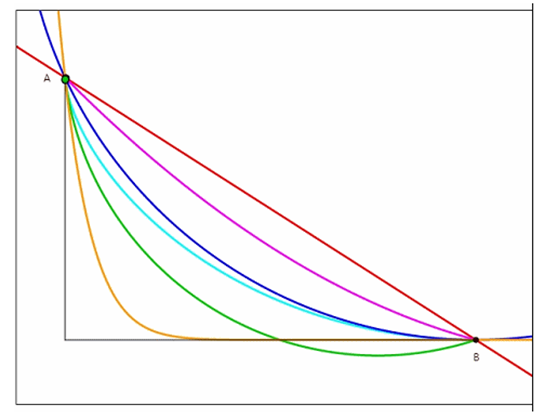
以上问题是一个经典的数学模型和实验。其问题的本质是在一个垂直平面内，一个质点在重力作用下，由静止出发从一个给定点A到不在它垂直下方的另一点B，如果不计摩擦力， 问该质点沿什么曲线滑下所需时间最短？

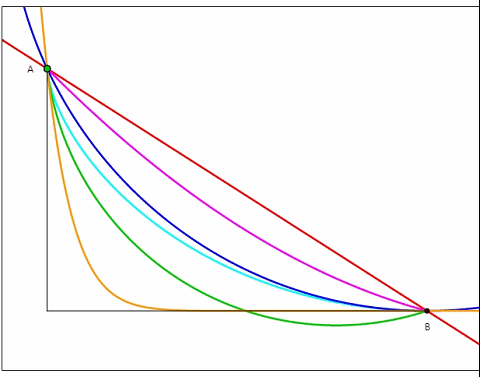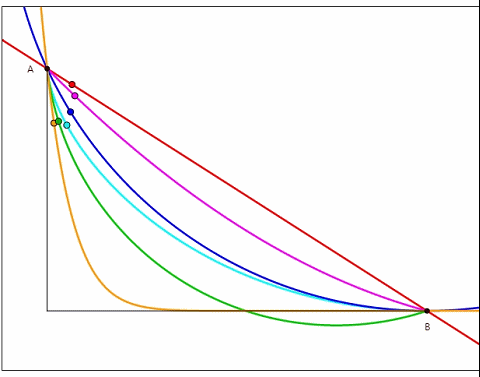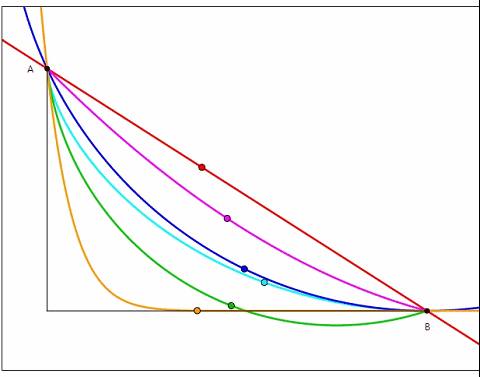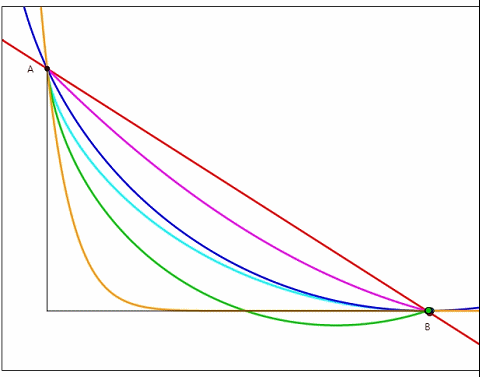
根据动图，我们清楚的发现浅蓝色的轨道从中胜出了？那么为什么是它呢？还有比它更快的曲线吗？这样的曲线又会满足什么样的性质呢？

这就是我们今天要为大家介绍的最速降线。

二、光学斯涅尔定律

在解决最速降线是何种曲线问题之前我们要准备一点“工具”。

在光学中，有个著名的斯涅尔定律，其表述是：光在同一均匀介质中沿直线传播，在不同介质中传播会发生折射。

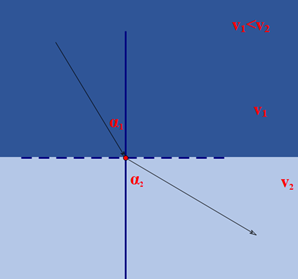
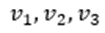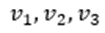图中不同颜色表示不同的介质，光在这些介质中的传播速度分别为，不妨设而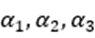分别表示光的人射角和折射角。

根据斯涅尔定律，在两层介质中有:

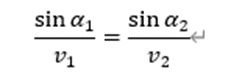
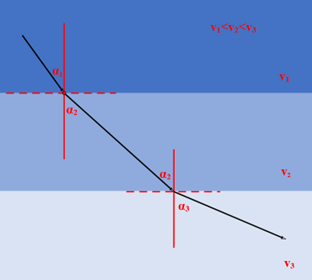
在三层介质中有:

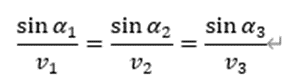
以此类推，在n层介质中有:

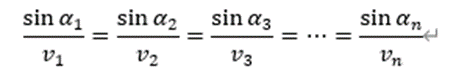
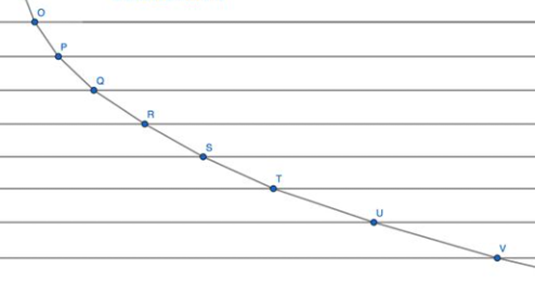
我们很容易想到，当n趋于无穷的时候，此时介质与介质之间距离非常细小，可以近似的认为介质的变化是连续的，在这样的一个过程中，光在其中的传播速度连续增加，并且形成了一条光滑的曲线。

这条曲线的特别之处在于曲线上的每一点都满足斯涅尔定律。在曲线上任取一点，设光在该点对应的介质中的传播速度为v，人射角为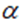，则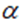即为曲线在该点处的切线与垂直方向的夹角，且有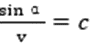，其中c为某一常数。

   三、最速降线方程建模与求解

如图所示建立平面直角坐标系：则最速降线就对应着一个函数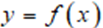。曲线上任意一点都应满足关系式:。

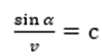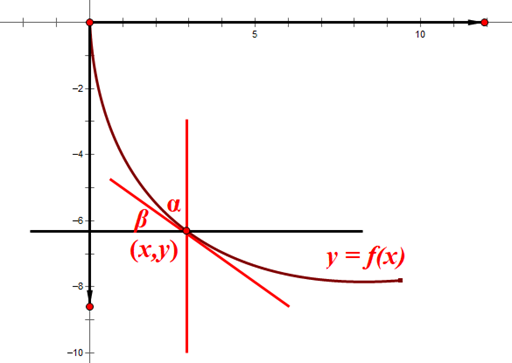
  根据能量守恒，得，即。再如图所示引人角度，由几何关系和导数的定义得 :将上述表达式代人:整理可得：即：。

这正是一个可分离变量的微分方程。在高等数学中我们学习了微分方程的概念和解法，同学们不妨拿出纸笔来计算一下上述方程的解。

从方程中解出，将原方程改写成显式的一阶微分方程：

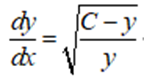
分离变量后，两边积分:

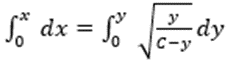
这里的具体求解过程如下图：

最终我们得到了最速降线的隐函数方程:

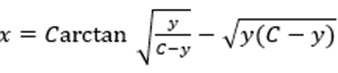
即只要沿着最速降线的方程曲线，我们就能做到从高处A最快下降到低处B。

四、生活中的最速降线

在刚结束的北京冬奥会上，中国选手谷爱凌夺得了自由式滑雪女U型场地技巧的金牌。这里的U形池也被设计成最速降线的形状，经验丰富的选手可以利用它得到最大加速，从而完成更高难度的动作。类似原理的还有过山车的轨道设计也参考了最速降线的性质。

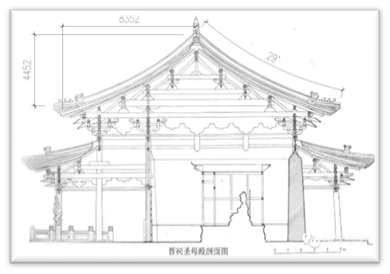
中国的许多古建筑，例如北京的故宫，山西太原的晋祠圣母殿，它们的屋顶结构中的瓦楞线的形状便是最速降线。瓦楞线条被设计成最速降线的形状，以保证雨水沿者它下落最快，减少雨水对建筑物的腐蚀。虽然古代的中国工匠们并不一定知晓最速降线，但是通过他们的智慧和工匠精神，却实践了现代科学的成果。