我们从中学开始就称e是自然对数，那么为什么要称其为自然对数呢？它的自然体现在哪里呢？
那么我们首先列举一个我们生活中和e有关的例子——理财产品的计息问题。假设某宝年利率高达100%，投人1万元，实行复利计息，计算一年后的本息和。
如果一年中计息一次，那么本息和：
如果一年中半年计息一次（一年计息两次），那么它的半年期利率为50%，那么本息和：
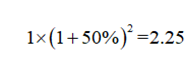
如果一年中每个季度计息一次（一年计息四次），那么它的每季度利率为25%，那么本息和：
从上面的计算中我们不难看出，计息周期不断缩小，虽然一个计息周期内的利率在变小，但是本息和是在不断增大的。
那么我们就有了这样一个问题，如果一年中的计息次数像这样无限拆分下去？每分钟，每秒钟都在计息，那么我们是不是会成为百万富翁呢？
我们根据上述问题，建立数学模型，假设年利率为100%，在一年中有n次计息周期，那么每期的利率就是
，那么一年之后它的本息和就是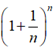
，如果计息周期n趋于无穷呢？若
，我们就将称为百万富翁！
但可惜的是，在《高等数学I》中我们已经学习了
是第二个重要极限，其极限值等于自然对数e。
我们回归正常的年利率，假设某宝年利率为5%，投入1万元，实行复利计息。假设1年内可无限次计息，求一年后的本息和。
解:若将一年平均分成n个时间段，则每个时间段的利率是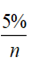
，一年后的本息和是
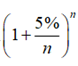，若考虑无限次计息，则有:
无限次计息条件下一年后的本息和是1.05127。
可见，在这种情况下，无限次计息与按年计息相比，一年后的本息和最多相差12.7元。
我们了解了生活中的e，那么e之所以称为自然对数，就在于自然界中存在了大量和e相关的现象。
我们在数学中将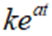
称为指数函数，这个表达式反映了很多自然现象，例如放射线性衰减、细菌的生长等。上述表达式我们也称为对数螺线，因为自然界中，银河系的结构，海螺等螺类生物的生长，一些植物的生长过程或形状就是以该螺线方程为基础。
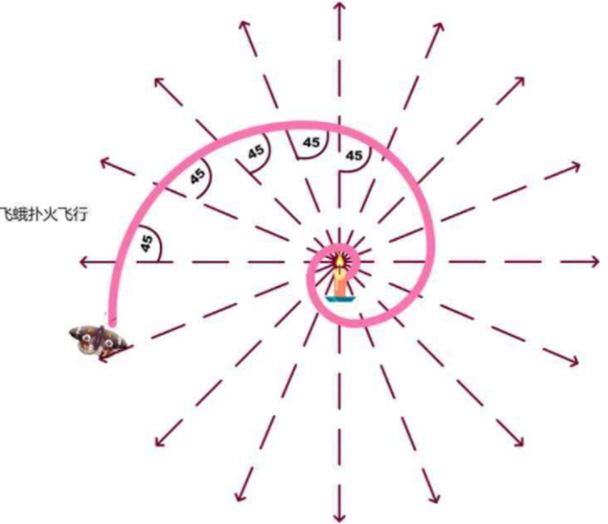
我们有一个成语叫做飞蛾扑火，那么我们有没有想过飞蛾为什么会有这样的行为呢？
我们假设飞蛾这辈子只能跟着光形成一个45°的夹角去飞行，由于太阳发出的光我们可以认为是一组平行光，那么他就会沿着直线飞行。
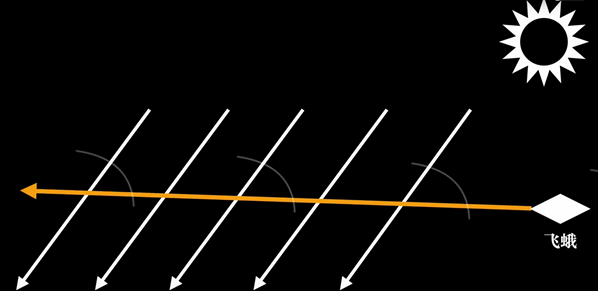
那么如果这时候是一盏烛火，我们知道烛火作为点光源，相当于从烛火发出了无数条光线，当飞蛾继续与光线保持固定角度飞行时，就会沿着一条等螺线飞向烛火。
