





2021-12-30 15:33:37 点击:[]
科学中的问题,常常起源于人们对大自然的研究。让我们观察一下下列自然事物--罗马花椰菜。(罗马花椰菜(Romanesco Broccoli),俗称青宝塔,属于十字花科芸薹属,它原本是一种普通的蔬菜,却吸引了无数的数学家和物理学家加以研究。)

我们任取其中一个“宝塔”,放大观察:

可以发现这个宝塔和原来的花椰菜居然如此相似。
再任取其中一个更小的“宝塔”,放大观察:

我们惊奇地发现,它和原来的花椰菜还有原来的“宝塔”都如此相似。如果继续上述步骤,会得到同样的结果。大自然竟创造出这样奇特,神秘又完美的事物!
其实这种“奇观”在神奇的大自然中,屡见不鲜,例如下面的植物花序、蕨类植物和叶脉:



1975年,当一位特立独行的波兰出生的数学家曼德勃罗(Benoit Mandelbrot)有了一个重要发现时,一个新词——分形(fractal)开始使用。那么什么是分形?为什么它们很重要?
所谓分形,分形之父曼德勃罗将其解释为“一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都是整体缩小后的形状。”
事实上,利用高中所学知识,我们可以构造结构最简单的一个分形图——著名的康托尔集。
取一个线段,把它中间的1/3去掉得到两个分开的线段,再对剩下的两段进行相同的操作,得到4个线段,这样重复进行下去直到无穷,最后得到的图形集合就是康托尔集。这样我们就用一个看似简单的步骤得到了一个无限复杂的图形,而且它的每一个细节放大之后都和整体看起来一样。

在1980年代,人们通过计算机制作的那些奇怪的、五颜六色的图案开始熟悉分形。
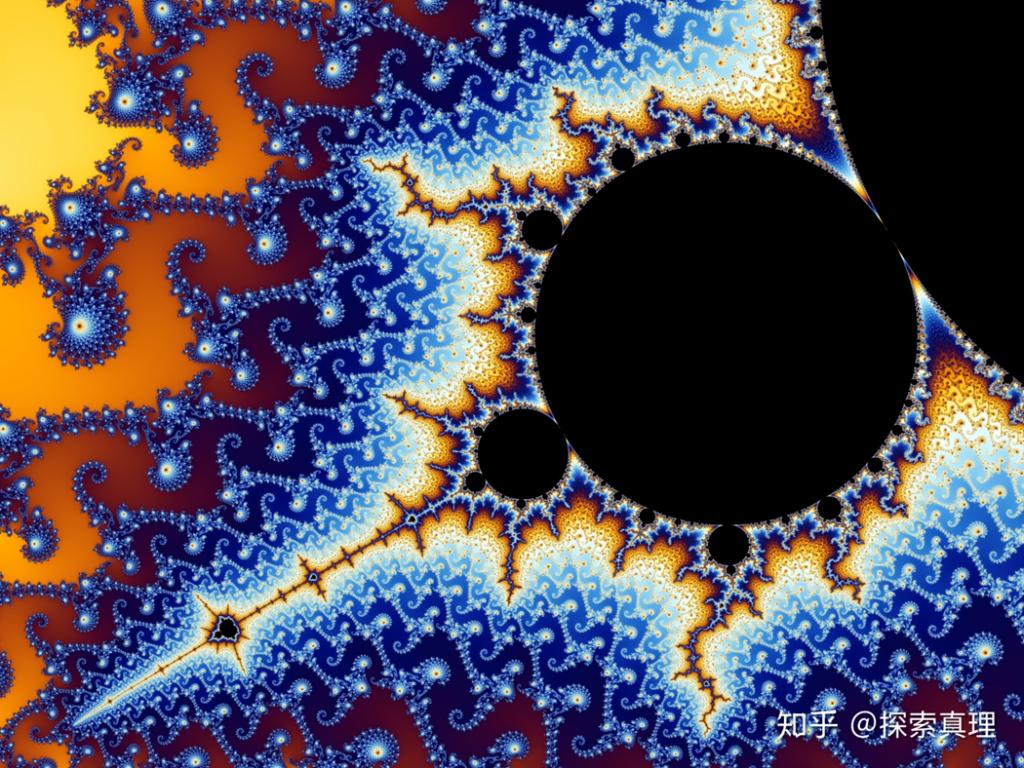
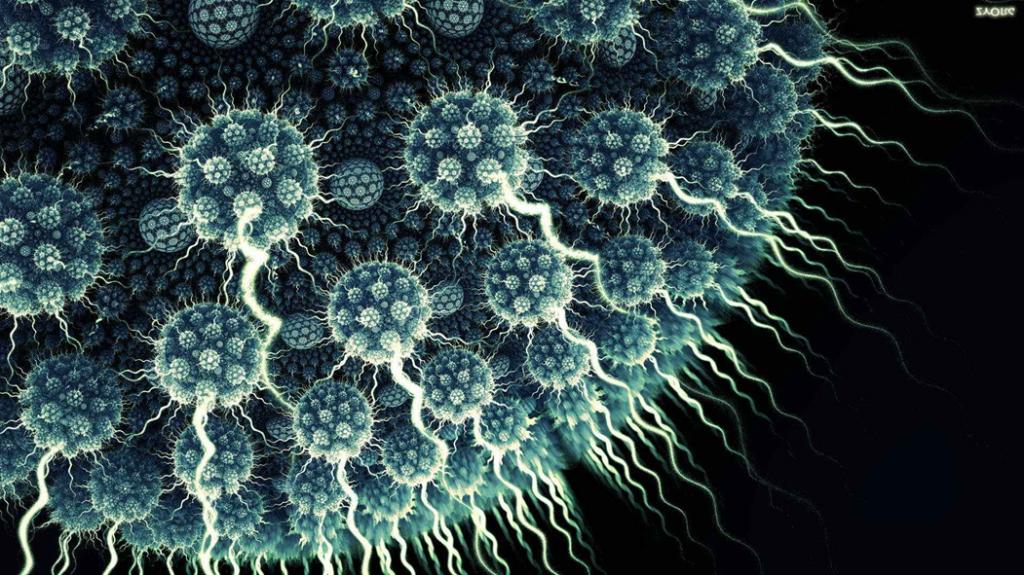
但很少有人意识到分形的概念如何彻底改变了我们对世界的理解,以及我们依赖于多少基于分形的系统。
分形的概念具有深刻的美感和力量,但就像现代科学和数学中的许多事情一样,分形没有既简单又准确的定义。
了解分形是什么的最好方法是考虑一些例子。雪花、云、山、海岸线、花椰菜和蕨类植物都是天然的分形。这些形状有一些共同点——直观、易于观察和美观。
曼德勃罗有句名言:“云不是球体,山不是圆锥体,海岸线不是圆,树皮不是光滑的,闪电也不是直线传播的。”
一朵云与其一小部分惊人地相似。一棵松树是由树枝组成的,而树枝又是由树枝组成的——而树枝又是由树枝组成的。山路上的小沙丘或水坑与山沟中的巨大沙丘和湖泊具有相同的形状。这种不同尺度的“自相似性”是分形的定义特征。
曼德勃罗开创的分形数学与混沌理论的相关领域一起揭开了世界隐秘之美的面纱。它启发了许多学科的科学家——包括宇宙学、医学、工程学和遗传学——以及艺术家和音乐家。曼德勃罗甚至认为整个宇宙都是分形的。
分形数学也有许多实际用途——例如,在制作令人惊叹和逼真的计算机图形、计算机文件压缩系统、构成互联网的网络架构中,甚至在诊断某些疾病方面。
分形几何还可以提供一种理解“系统”以及形状复杂性的方法。地震的时间和大小以及人的心跳的变化和疾病的流行仅仅是分形几何可描述的不可预测的三种情况。
另外在金融市场,曼德勃罗在1960年代担任IBM研究员时首次尝试使用分形数学来描述市场,根据交易者随着时间的推移而产生的利润和损失,并发现它运作良好。
因此,分形提醒我们,这个世界是复杂的美妙的,但又是相互联系的。